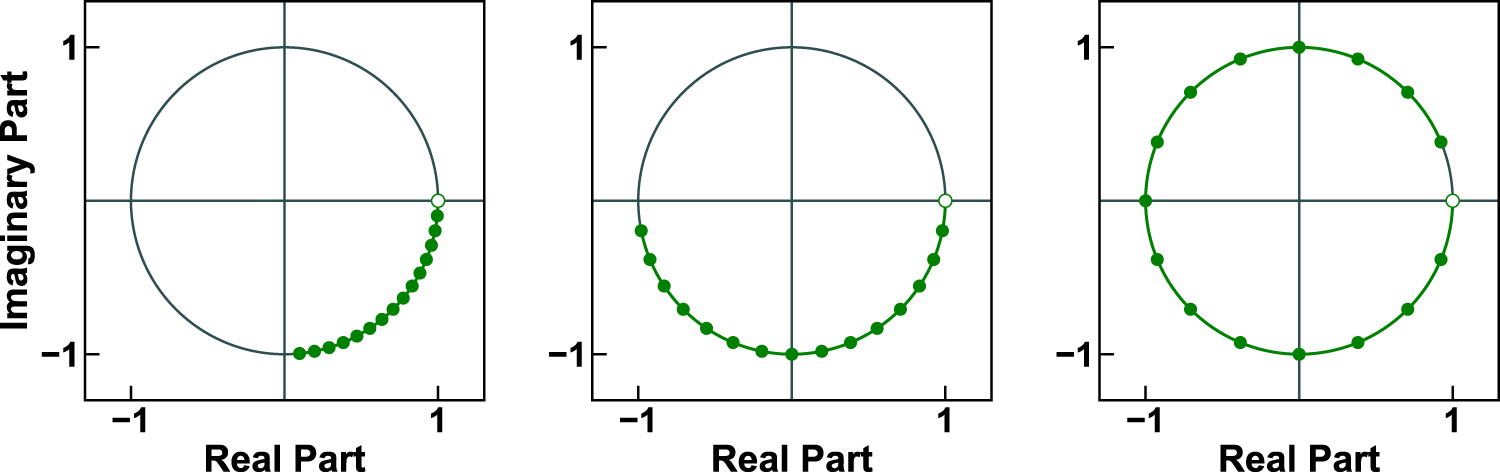
Here are three examples of 16-point chirp contours on the unit circle. The ICZT algorithm developed by Iowa State engineers can work with all three while the one previously used can work only with the last contour. Figure courtesy of Alexander Stoytchev.
Engineers explore algorithm’s capabilities in special cases ‘on the unit circle’
AMES, Iowa – Iowa State University’s Alexander Stoytchev says it’s one of the “most popular and useful” algorithms around – even though most of us have never heard of it.
But, if you’ve used a cell phone, browsed the internet or needed a medical image, you’ve benefitted from the fast Fourier transform (FFT).
The transform and its inverse (known as the IFFT) have been in use since 1965. For example, in your cell phone the FFT is used to analyze the signal received from the base station (or cell tower). The IFFT solves the inverse problem: it synthesizes the signal that your phone sends to the base station.
In 1969, researchers developed a more useful, generalized version of the FFT known as the chirp z-transform (CZT). But nobody had come up with a generalized version of the IFFT. It was a 50-year-old puzzle in signal processing.
That is, until last fall when two Iowa State engineers – Stoytchev and Vladimir Sukhoy – announced in a research paper they had come up with a closed-form solution for the inverse chirp z-transform (ICZT) and a fast algorithm for computing it. (The paper sparked a lot of interest in the signal-processing community, tallying more than 26,000 accesses since October.)
Now Stoytchev – an associate professor of electrical and computer engineering who’s also affiliated with the university’s Virtual Reality Applications Center – and Sukhoy – a lecturer in electrical and computer engineering – report new research results about their algorithm.
In a paper just published online by Scientific Reports, a Nature Research journal, the two show how their algorithm functions “on the unit circle,” which refers to a special case of its parameters. (Their previous paper only highlighted operations “off the unit circle.”)
The paper details how the algorithm can work with frequency components that are generated by sample points from the unit circle in the complex plane. These points form a contour that is known as the chirp contour. Unlike the IFFT, which can only work with equispaced sampling points that fully cover the unit circle, the ICZT algorithm can work with contours that cover only a fraction of the unit circle. It can also work with contours that wrap around and perform multiple revolutions over the circle. This enables the use of certain (non-orthogonal) frequency components, which lifts one of the main restrictions of the IFFT and could lead to better spectrum utilization.
The paper identifies the parameter values for which the algorithm is numerically accurate and for which it isn’t, and describes how to estimate its accuracy as a function of the parameters. (Technical note: It shows that the singularities of the ICZT of size n are related to the elements of the Farey sequence of order n-1. This is an interesting connection because Farey sequences often appear in number theory.)
The paper demonstrates that, on the unit circle, the ICZT algorithm achieves high accuracy with only 64-bit floating-point numbers and does not require additional numerical precision, making it easier to implement. It reports the algorithm can pair well with the existing CZT algorithm to do back-to-back signal analysis and signal synthesis. And it shows that the algorithm is fast (it operates in what’s known as O(n log n) time).
“This algorithm is more general than the IFFT, but maintains the same speed,” Stoytchev said.
That’s good news for the engineers working to solve all kinds of signal-processing challenges:
“Application domains that could benefit from this,” the Iowa State engineers wrote in the paper, “include signal processing, electronics, medical imaging, radar, sonar, wireless communications, and others.”
Contacts
Alexander Stoytchev, Electrical and Computer Engineering, Virtual Reality Applications Center, alexs@iastate.edu
Mike Krapfl, News Service, 515-294-4917, mkrapfl@iastate.edu
Read the papers
New Paper:
"Numerical error analysis of the ICZT algorithm for chirp contours on the unit circle," Scientific Reports, 10, 4852 (2020).
Previous paper:
"Generalizing the inverse FFT off the unit circle," Scientific Reports, 9, 14443 (2019).
Quote
“Application domains that could benefit from this include signal processing, electronics, medical imaging, radar, sonar, wireless communications, and others.”
Alexander Stoytchev and Vladimir Sukhoy, writing in Scientific Reports
Quick look
Two Iowa State engineers, who announced the solution to a 50-year-old puzzle in signal processing last fall, have followed up with more research results. The engineers say their new algorithm is more useful and just as fast as the one previously used.